شما اینجا هستید
یک مثال شبکه عصبی با سه لایه و ضرب ماتریس
ما تا الان از ماتریس ها برای محاسبه سیگنال های شبکههای عصبی استفاده نمی کردیم. همچنین تا حالا با مثالهایی بیشتر از دو لایه هم کار نکردیم. این مثالها جالب بودند به خاطر اینکه ما نیاز داشتیم ببینیم خروجی های لایه میانی را به عنوان ورودی لایه سوم استفاده کنیم.
تصویر زیر یک مثال از شبکه عصبی با سه لایه را نشان میدهد.در هر لایه سه گره وجود دارد. برای اینکه تصویر واضح باشد همه وزن ها را ننوشتیم.
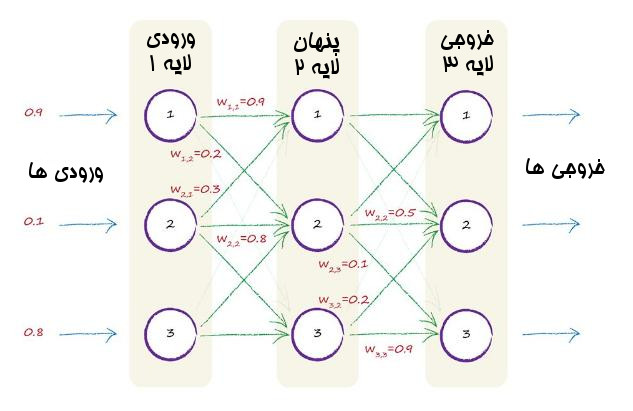
ما در اینجا چند اصطلاح خیلی رایج را نیز به کار بردیم. لایه اول با نام لایه ورودی شناخته می شود. همانطور که قبلاً می دانستیم. لایه آخر هم که میدانیم لایه خروجی است. لایه وسط با نام لایه پنهان شناخته می شود. به نظر راز آلود می آید. اما متأسفانه هیچ رازی در کار نیست. به خاطر این اسمش پنهان است که خروجی این لایه مستقیم به عنوان خروجی در دسترس نیست. پس پنهان است. خیلی قانع کننده نیست. ولی خوب دلیل بهتری برای این نام وجود ندارد.
بیایید روی این شبکه که در تصویر میبینیم کار کنیم. ما سه مقدار ورودی به نام 0.9 و 0.1 و 0.8 داریم بنابراین ماتریس ورودی یعنی I ما برابر است با

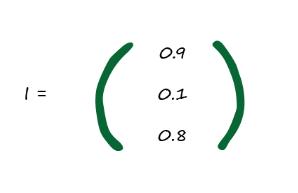
خوب خیلی آسان بود. کار لایه اول تمام شد. این همه کاری است که در لایه ورودی انجام میدهیم. این لایه فقط نشان دهنده مقادیر ورودی است.
بعدی لایه وسط یا همان لایه پنهان است. اینجا ما نیاز به ضرب و تعدیل و جمع سیگنال ها به ازای هر گره در لایه میانی داریم. به خاطر بیاورید که هر گره در لایه میانی به هر گره در لایه ورودی متصل است. برای همین هم بخشی از هر سیگنال ورودی را دریافت می کند. نمیخواهیم مثل حالت قبل محاسبات زیادی انجام دهیم. میخواهیم از روش ماتریس استفاده کنیم.
همانطور که قبلتر دیدیم ، ترکیب و تعدیل ورودی ها در این لایه میانی با فرمول
X=W.I
انجام میشود که در اینجا I ماتریس سیگنال های ورودی بود. و W ماتریس سیگنال های وزن بود.
خوب I داریم ولی W را چه کار کنیم؟ تصویر تعدادی از ورودی ها را برای ما نشان داده است. اما همه آنها مشخص نیستند. ماتریس زیر همه آنها را نشان میدهد.دوباره باید تأکید کنیم که این مقادیر به صورت تصادفی انتخاب شده اند. چیز خاصی در مورد آنها در این ماتریس وجود ندارد.
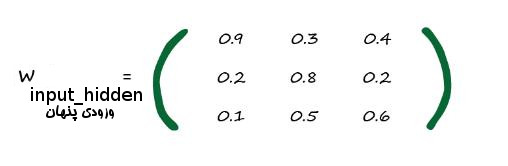
شما میتوانید وزن های بین اولین گره از لایه ورودی و اولین گره از لایه پنهان را ببینید. این مقدار برابر است با
w1,1=0.9
این همان چیزی است که در تصویر بالا نیز نمایش داده شده است. شبیه این شما میتوانید وزن ارتباط بین گره دوم ورودی و گره دوم لایه پنهان را نیز ببینید که برابر است با
w2,2=0.8
در تصویر اولیه بالا ارتباط بین گره سوم ورودی و گره اول لایه پنهان نشان داده نشده است . در اینجا این مقدار را میبینیم که برابر است با:
w3,1=0.1
اما صبر کنید. چرا ما یک «ورودی پنهان» جلوی W گذاشتیم؟ به خاطر اینکه Winput_hidden وزن های بین ورودی و لایه پنهان است. ما به یک ماتریس دیگر از وزن ها نیز نیاز داریم که ارتباط بین لایه پنهان و لایه خروجی است. میتوانیم آن را Whidden_output بنامیم.
در زیر ماتریس دوم یا همان ماتریس Whidden_output آمده است. وزن ها را از قبل پر کردیم. دوباره دقت کنید که برای مثال ارتباط بین گره سوم لایه پنهان و گره سوم لایه خروجی مقدار به این شکل است:
w3,3=0.9
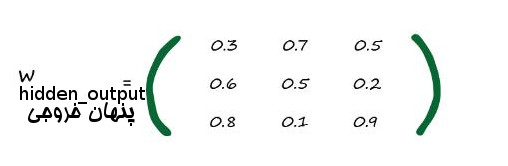
عالی. ما ماتریس وزن های مورد نیازمان را داریم. اجازه بدهید با کار کردن روی جمع ورودی های تعدیل شده در لایه پنهان آغاز کنیم.یک نام مختصر برایش میگوییم که بدانیم منظورمان دادههایی است که به عنوان ورودی به لایه پنهان وارد میشوند نه اینکه به لایه آخر وارد شوند. خوب نام آن را میگذاریم Xhidden .
Xhidden=Winput_hidden·I
خوب در اینجا کل عملیات ضرب ماتریس ها را انجام نمی دهیم. به خاطر اینکه موضوع کلاً ضرب یک ماتریس است ما از کامپیوتر ها برای انجام اینطور کارها استفاده می کنیم. پاسخ در زیر آمده است.

من از یک کامپیوتر برای این کار استفاده کردم. ما در بخش دو از این راهنما با هم یاد میگیریم که چطور با استفاده از زبان برنامه نویسی پایتون این کار را انجام دهیم. این کار را الان انجام نمیدهیم چون نمیخواهیم در این قسمت با نرمافزار های کامپیوتری کار کنیم.
خوب حالا ما ورودی های تعدیل شده لایه پنهان میانی را داریم. آنها 1.16 و 0.42 و 0.62 هستند. ما از ماتریس ها خواستیم که قسمت سخت کار را برای ما انجام دهند. این دستاورد مایه مباهات است. بیایید این ورودی های تعدیل شده و جمع شدن در لایه دوم را به تصویر بکشیم:
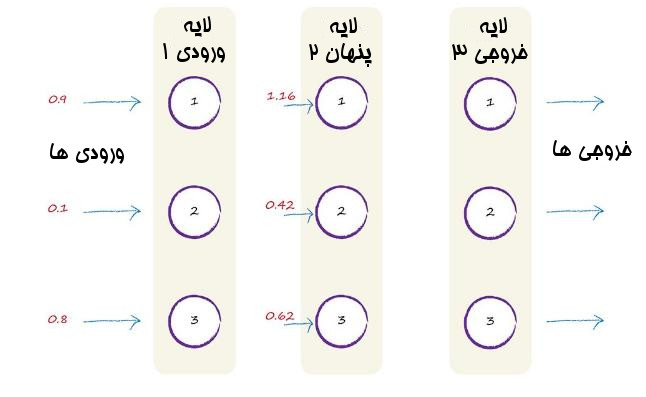
تا حالا که خوب بوده. اما کارهای بیشتری برای انجام است. به خاطر داریم که به ازای هر گره ما بیاد تابع فعال سازی سیگموئید را روی آن اعمال کنیم. این کار برای این بود که خروجی ما شبیه به رفتار طبیعت و نرون های زیستی شود.
خوب بیایید آن را انجام دهیم:
Ohidden=sigmoid(Xhidden)
تابع سیگموئید بر روی هر عنصر در ماتریس Xhidden اعمال می شود. تا در نهایت خروجی لایه پنهان وسط تولید گردد.
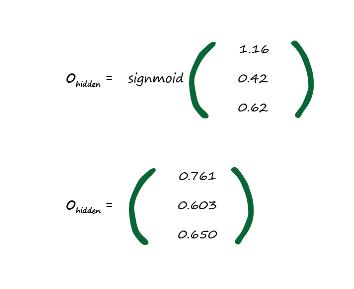
بهتر است اولین عنصر را بررسی کنیم تا مطمئن شویم. تابع سیگموئید برابر است با
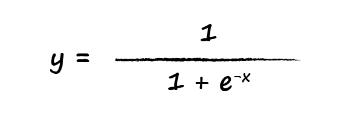
بنابراین
x=1.16
e-1.16=0.3135
y=1/(1+ 0.3135)=0.761
میتوانید ببینید که همه مقادیر بین صفر تا یک هستند. به دلیل اینکه تابع سیگموئید عددی خارج از این رنج را تولید نمی کند. میتوانیم به نمایش گرافیکی تابع لوجستیک برگردیم تا این موضوع را مشاهده کنیم.
پفففف… بیایید همینجا دست نگه داریم و ببینیم تا الان چه کار کرده ایم. ما روی سیگنال های ورودی به لایه میانی کار کردیم تا خروجی لایه میانی را به دست آوریم. که خیلی هم واضح بود.مقادیر ورودی را در وزن آنها ضرب کردیم ، همه را با هم جمع کرده و در نهایت تابع فعال ساز را روی آن پیاده کردیم. بیایید این تصویر را با این اطلاعات پر کنیم.
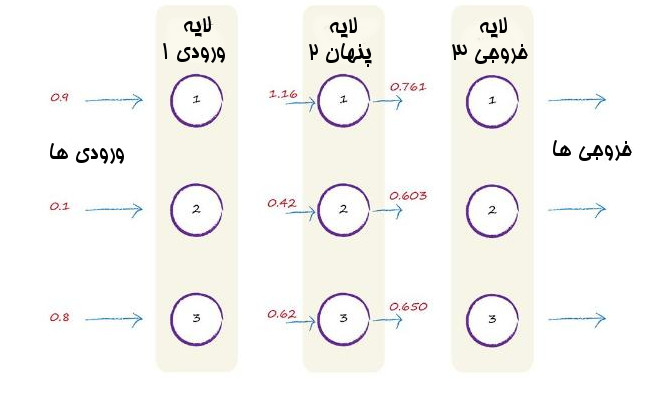
اگر این یک شبکه عصبی دو لایه بود. کار همین جا تمام میشد. اما باتوجه به سه لایه بودن این شبکه کار ما این اینجا تمام نمی شود. ما لایه سومی هم داریم.
چطور روی سیگنال های لایه سوم کار کنیم؟ مثل لایه دوم. تفاوتی وجود ندارد. ما در اینجا یعنی لایه سوم هم سیگنال ورودی داریم. که از خروجی لایه دوم آمده اند.
همچنین بین این اتصال ها وزن هایی وجود دارند که اتصال ها را تعدیل می کنند. همینطور تابع های فعال سازی داریم که با روی سیگنال ها اعمال میشوند و کار نورون را شبیه به یک نوروی زیستی می کنند.
خوب یک چیز را باید به خاطر داشته باشیم. بدون توجه به اینکه چه تعداد لایه داریم، ما میتوانیم هر لایه را مثل بقیه در نظر بگیریم. ما ورودی های سیگنالی که در وزن های آنها ضرب شده را با هم جمع میکنیم و در نهایت تابع فعال سازی را روی آنها اعمال می کنیم.در نهایت با اعمال تابع فعال سازی ما خروجی لایه را داریم.
بدون توجه به اینکه در حال کار روی لایه سوم هستیم یا ۵۳ ام یا ۱۰۳ام روش یکسان است.
خوب بیایید معادله X=W.I را روی این لایه هم اعمال کنیم. مثل کاری که قبل تر کردیم.
ورودی های این لایه خروجی های لایه قبل یعنی لایه دوم هستند. که ما در بالا محاسبه کردیم . یعنی همان Ohidden . و وزن های بین این لایه و لایه دوم به نام Whidden_output را هم داشتیم. هر لایه ماتریس وزن های خودش را دارد و با آنی که بین لایه اول و دوم استفاده کردیم یکی نیست. بنابراین ما داریم:
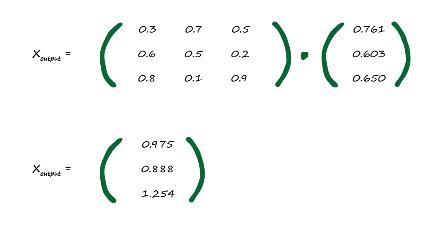
Xoutput=Whidden_output·Ohidden
بنابراین با محاسبه آن ما مقادیر تعدیل شده و جمع شده لایه سوم را داریم.
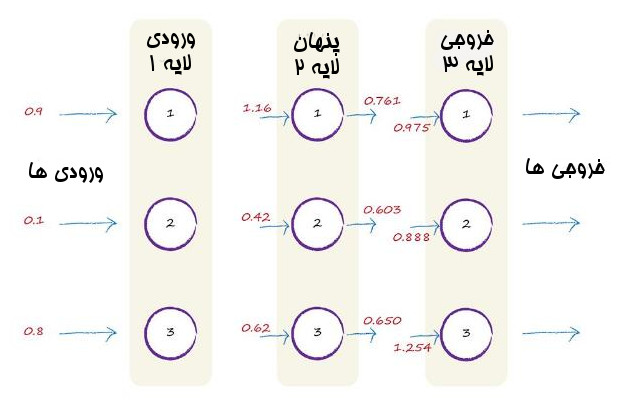
تصویر زیر روش پیش رفت به سمت جلو سیگنال را ها از ورودی اولیه تا ورودی جمع و تعدیل شده در لایه آخر را نشان می دهد.
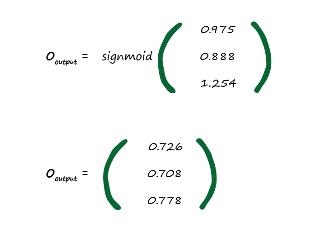
تنها چیزی که میماند اعمال تابع فعال سازی سیگموئید است که کار آسانی است.
خودشه. ما بالاخره خروجی نهایی را از شبکه عصبی مان گرفتیم بیایید آن را در تصویر بیاوریم
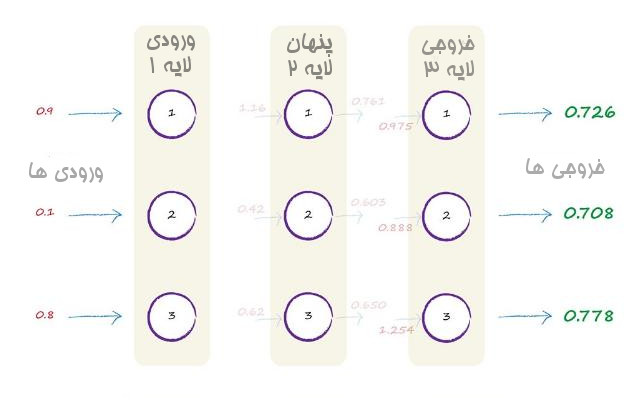
بنابراین خروجی نهایی مثال شبکه عصبی ما در سه لایه برابر با مقادیر
0.726 , 0708 ,0.778
است.
ما با موفقیت از سیگنال ورودی در شبکه عصبی و گذر از لایه ها توانستیم در نهایت از لایه خروجی یک یک سری مقدار خروجی بگیریم.
خوب حالا چی؟
مرحله بعد این است که از این خروجی شبکه عصبی برای مقایسه با دادههای آموزش استفاده کنیم. ما نیاز داریم که خطا را محاسبه کنیم و آن را کاهش دهیم و شبکه عصبی را جوری تنظیم کنیم که خودش را بهبود دهد و خطا های خروجی به حداقل برسد.
این شاید سخت ترین چیزی باشد که باید یاد بگیریم. بنابراین ما به آرامی پیش میرویم و ایده هایمان را پیاده می کنیم.



دیدگاهها
پس انتشار
با سلام و احترام و تشکر از
دیدگاه جدیدی بگذارید