شما اینجا هستید
یک دستگاه پیشبینی ساده
بیایید از یک جای خیلی ساده شروع کنیم و از آنجا همه چیز را بسازیم.
یک ماشین خیلی ساده را تصور کنید که یک سؤال را دریافت می کند، مقداری فکر میکند و یک جواب می دهد. مثل مثال تشخیص تصویر که چشمهای ما یک چیز را میبیند ، صحنه را بررسی می کند. در انتها به این نتیجه میرسیم که چه چیزهایی در تصویر وجود دارد.
اگر بخواهیم یک نمودار برای آن ترسیم کنیم شاید چیزی شیبه زیر شود:

واقعیت این است که کامپیوتر ها فکر نمی کنند، آنها تنها فقط ماشین حسابهایی هستند که حافظه هم دارند. پس بیایید نمودار بالا را با اصطلاحات مناسب دوباره ایجاد کنیم.

یک کامپیوتر تعدادی ورودی میگیرد، تعدادی محاسبه انجام میدهد و بعد یک خروجی می دهد. مثالی برای واضح شدن موضوع می نویسیم. یک ورودی مثلاً ۳*۴ را در نظر بگیرید، شاید در کامپیوتر این ضرب به حالت سادهتری مانند مجموعه از جمع ها تبدیل میشود و سپس خروجی ۱۲ بیرون میآید

خوب قطعاً خیلی تحت تأثیر قرار نگرفتیم. شاید با خود فکر میکنید که ما داریم یک مثال واضح آشنا میزنیم تا بعد ها آن را در شبکه عصبی جالب خود به کار ببریم.
بیایید با یک قدم کوچک کمی به پیچیدگی موضوع اضافه کنیم.
تصور کنید یک دستگاه داریم که کیلو متر را به مایل تبدیل می کند. این دستگاه فرمول تبدیل کیلومتر به مایل را نمی داند. همه ما میدانیم که رابطه بین این دو خطی است
یعنی یک کیلومتر تقریباً برابر با 0.62 مایل است.
یعنی دو کیلومتر تقریباً برابر با 1.24 مایل است و به همین ترتیب
یعنی اگر مقدار به مایل را دو برابر کنیم مقدار به کیلو متر نیز دو برابر میشود و برعکس
همین رابطه خطی به ما یک دیدگاه برای شروع به کار می دهد.
.از آنجایی که رابطه بین این دو خطی است فرمول آن باید چیزی شبیه به این باشد
مایل = کیلومتر * یک عدد ثابت
یا به انگلیسی
miles= kilometers * constant number
یا به صورت خلاصه
m = k * c
البته ما نمیدانیم این عدد ثابت یعنی همانی که جایش c گذاشتیم چه مقدار است
یک سرنخ دیگری که داریم این است که تعدادی مثال از کیلومتر و معادل های آنها در مایل را داریم. درست مثل دنیای واقعی است. جایی که ما از نمونههای که در اطراف مشاهده می کنیم و یا در آزمایشگاه با ثبت مقدار های یک رویداد، الگو ها را استخراج میکنیم و نتیجهگیری می کنیم.
|
شماره مشاهده قابل اطمینان و معتبر |
کیلومتر |
مایل |
|
۱ |
۰ |
۰ |
|
۲ |
۱۰۰ |
۶۲.۱۳۷ |
چون قرار نیست در این فصل برنامهای بنویسم ذکر این نکته لازم است که:
اگر قرار بود برنامهای بنویسیم ، میبایست شبکه عصبی می نوشتیم که بتواند رابطههای بین مشاهداتی که به صورت خطی با هم در ارتباط هستند را از روی مشاهدات بتواند کشف کند.
ذهن ما نیز میتواند در رابطههای خطی با تعداد خیلی کمی از مشاهده از یک رویداد به سرعت عدد ثابت را به صورت تقریبی حدس بزند. اگر مشاهده جدیدی ببیند سریع بررسی کند که آیا آن عدد ثابت در این مشاهده جدید نیز کارکرد دارد یا خیر اگر نه آن را اصلاح کند.
در اینجا برای شروع یک عدد تصادفی بر میداریم مثلاً ۰.۵ و ببینیم رابطه با آن کار میکند یا نه

در اینجا ما عدد ثابتی که حدس میزدیم را در معادله مایل = کیلومتر * یک عدد ثابت قرار دادیم. بعد آن را مشاهده ی های قبلی تطبیق می دهیم. اکنون برای صد کیلومتر به پنجاه مایل رسیدیم .
خوب برای شروع بد نیست، اما مقادیر خیلی هم صحیح نیست. در مشاهده دو دیدیم که این مقدار باید ۶۲.۱۳۷ باشد.
میزان خطای ما از مشاهده در اینجا برابر ۱۲.۱۳۷ است.که از این فرمول آن را به دست آوردیم
میزان خطا = عدد مشاهده شده – عدد محاسبه شده
یعنی در اینجا
۶۲.۱۳۷-۵۰
برابر میشود با
۱۲.۱۳۷
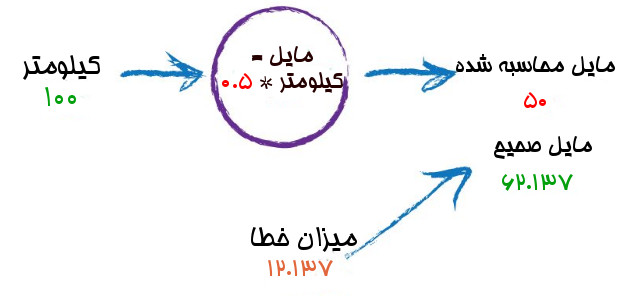
حالا بعد چی؟ میدانیم که مقداری خطا داریم به جای اینکه نا امید شویم بیایید از این موضوع به عنوان یک راهنما استفاده کنیم و یک بار دیگر حدس بزنیم. از آنجایی که رابطه بین کیلومتر و مایل خطی است ما میدانیم با افزایش مقدار ثابت یا همان c عدد خروجی بزرگتر می شود.
حالا مقدار ثابت را از ۰.۵ به ۰.۶ افزایش دهیم و ببینیم چه می شود.
با تغییر مقدار ثابت به ۰.۶ و قرار دادن آن در رابطه داریم
۱۰۰* ۰.۶ =۶۰
خوب ۶۰ خیلی بهتر از عدد قبلی یعنی ۵۰ است و نزدیکتر به مقدار مشاهده ما است. به وضوح پیشرفت داشتیم. حالا خطا شد ۲.۱۳۷ که خیلی کوچکتر شد. حتی میتوانیم این مقدار خطا را هم نادید بگیریم.
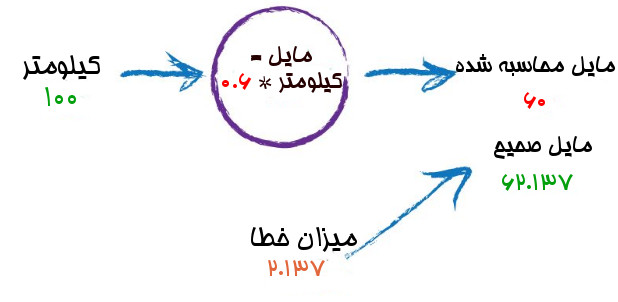
نکته کلیدی ماجرا اینجاست که ما از محاسبه میزان خطا برای تغییر دادن عدد ثابت و به دست آوردن عدد صحیحتر استفاده کردیم ما میخواستیم خروجیمان که ۵۰ بود را کمی افزایش دهیم، پس مقدار عدد ثابت را کمی بیشتر کردیم.
مهمترین نکته تمام مطالب گفته شده در بالا این مطلب است که:
ما به جای اینکه از جبر و ریاضی برای بدست آوردن مقدار دقیق عدد ثابت استفاده کنیم از روش سعی و خطا استفاده کردیم. اگر فکر می کنید که این کار بیهوده است و روش معادله خیلی راحت تر جواب می دهد، دقت داشته باشید خیلی که رابطه ها در جهان به صورت خطی نیستند. پارامتر های زیادی دارند و به آسانی نمی توان برای آنها فرمول خاصی پیدا کرد. به همین دلیل ما نیاز به شبکه های عصبی داریم.
اجازه بدهید این کار را دوباره انجام دهیم
خروجی ۶۰ هنوز هم کوچک است
خوب حالا بیایید عدد ثابت را به ۰.۷ افزایش دهیم.
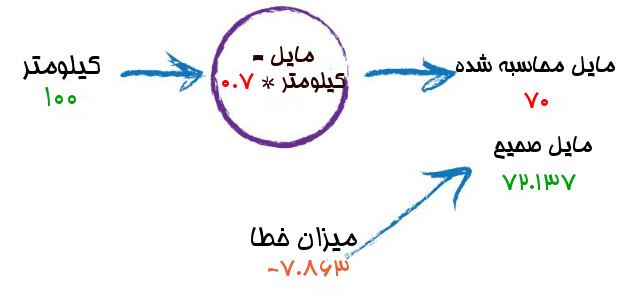
عجب کاری شد. زیادی عدد ثابت را بالا گرفتیم. خروجی قبلی خیلی نزدیکتر به مشاهده بود. همینطور خطای ما در قبل عدد ۲.۱۳۷ بود که حالا شد -۷.۸۶۳ . علامت منفی در خطا به خوبی نشان میدهد که مقدار به دست آمده بزرگتر بوده و زیادی جلو رفتیم. به خاطر بیاورید که میزان خطا از این رابطه به دست می آمد.
میزان خطا = مقدار واقعی – مقدار محاسبه شده
خوب همان عدد ثابت ۰.۶ خیلی بهتر از ۰.۷ بود میتوانیم فکر کنیم به نتیجه رسیدیم. اما بیایید یک تلاش دیگر بکنیم. این بار عدد ثابت را کمی افزایش میدهیم. بیایید آن را از ۰.۶ به ۰.۶۱ افزایش دهیم
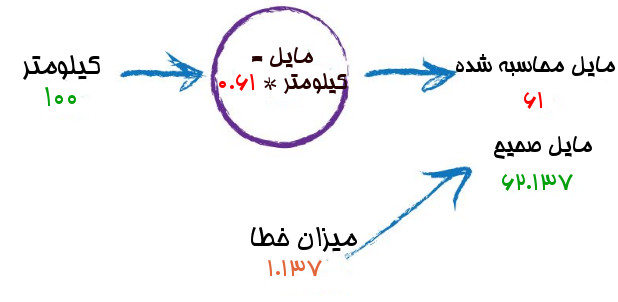
خیلی بهتر از قبل شد. حالا خروجی ما ۶۱ است که میزان خطایی به اندازه ۱.۱۳۷ از مقدار مشاهده که ۶۲.۱۳۷ است دارد.
تلاش قبلی به ما یاد داد که باید میزان تغییر در عدد ثابت را کوچکتر کنیم. اگر خروجی به مشاهده نزدیکتر شود، خطا کوچتر می شود. از روی عدد خطا میتوانیم بفهمیم که غلط نفرفتیم.
همینطور بدون اینکه خسته بشویم عدد ثابت را تصحیح می کنیم. همینطور به میزان خطا نگاه میکنیم اگر عدد خطا بزرگ بود یعنی اینکه نیاز به تغییر بزرگتری در عدد ثابت داریم. اگر عدد خطا کوچک بود یعنی میزان کمی تغییر در عدد ثابت را نیاز داریم و اینکه داریم به نتیجه می رسیم.
آنچه که ما اینجا انجام دادیم، باور کنید یا نه، هسته اصلی اتفاقاتی است که در شبکه عصبی روی می دهند. ما یک ماشین را به این شکل آموزش میدهیم که با توجه به مشاهدات خودش را در دادن خروجی صحیح بهتر و بهتر کند.
مهمترین نکتهای که باید به آن توجه کنید این است که ما مثل آموزشهای ریاضی در مدرسه در یک مرحله مسأله را حل نمی کنیم. چیزی که در تمام طول دوره تحصیل در کلاسهای ریاضی به ما یاد داده می شود. در عوض یک پاسخ پیدا میکنیم و سعی میکنیم آن را با تکرار بهبود دهیم
بعضی برای این حالت از اصطلاح ایتریتیو(iterative) استفاده میکنند و منظورشان این است که ذره ذره با تکرار خروجی را بهبود ببخشیم.
نکته های کلیدی:
تمام کامپیوتر ها دارای ورودی و خروج هستند. در داخل آنها محاسبات انجام می شود. شبکه های عصبی هم از این قائده مستثنی نیست.
وقتی نمیدانیم چه کار باید بکنیم، سعی می کنیم آن را در یک مدل قرار دهیم و با پارامتر های آن بازی کنیم
مثلا وقتی نمیدانستیم چطور کیلومتر را به مایل تبدیل کنیم، یک تابع خطی را در نظر گرفتیم و شیب آن را تنظیم کردیم.
یک راه درست برای این کار این است که پارامتر ها را بر اساس خطای بدست آمده بین محاسبات و مقدار مثالی که داریم تغییر دهیم



دیدگاه جدیدی بگذارید