شما اینجا هستید
چطور واقعا وزن ها را بروز میکنیم؟
تا اینجا هنوز به موضوع اصلی که همان بروزرسانی وزن های لینک ها در شبکههای عصبی است ورود نکردیم. فکر کنم الان دیگر وقت آن است و به این نقطه رسیدیم.تنها یک کلید دیگر کافی است تا بتوانیم قفل این راز را باز کنیم.
تا اینجا ما خطا ها را به تمام لایهها به عقب انتشار دادیم. چرا این کار را کردیم؟ به خاطر اینکه از این مقادیر خطا به عنوان راهنمایی برای تنظیم و اصلاح وزن ها استفاده می کنیم. با این کار مجموعاً پاسخ شبکه را بهبود می دهیم. این همان کاری است که در ابتدای این راهنما روی دسته بندی کننده خطی آن را انجام دادیم.
اما این گرهها دسته بندی کننده ساده خطی نیستند. آن گرهها یک مقدار پیچیدهتر هستند. به این شکل که هر گره سیگنال های وزن دار ورودی را جمع زده و روی آنها تابع سیگوئید را اعمال می کند. خوب چطور واقعاً وزن های اتصال های این گرههای پیچیده را بروزرسانی می کنیم؟ خوب چرا از یک تابع سرراست استفاده نکنیم که مشخص کند هر وزن چقدر باید باشد؟
ما نمیتوانیم از یک تابع مستقیماً برای محاسبه و بروز رسانی وزن ها استفاده کنیم. دلیل آن این است که ریاضیات آن خیلی پیچیده می شود. ترکیب زیادی از وزن ها داریم. همچنین تابع های زیادی داریم که ورودی آنها یک تابع است. یک شبکه با سه لایه که در هر لایه تنها سه نورون وجود دارد را در نظر بگیرید. مانند مثالهایی که قبلتر داشتیم. چطور وزن بین ورودی گره اول لایه ورودی و گره اول لایه دوم یا همان پنهان را تنظیم کنیم. مثلاً وقتی که یک بار تا انتها رفتیم و برون داد گره سوم لایه خروجی برابر 0.5 می شود؟
برای تصور اینکه چقدر اینکار سخت است، فقط به عبارت وحشتناک زیر نگاه کنید: این فرمول خروجی گره های لایه خروجی به عنوان یک تابع از ورودی های تابع ورودی و همچنین وزن پیوند ها برای یک شبکه عصبی ساده 3 لایه با 3 گره در هر لایه را نشان می دهد.

خوب اجازه بدهید که این فرمول را اصلاً نفهمیم و از کنارش رد شویم
در عوض سعی میکنیم خیلی باهوش باشیم ، خوب اگر سعی کنیم ترکیبی تصادفی از وزن ها را ایجاد کنیم تا زمانی که به یک نسخه خوب از آنها برسیم چی؟
همیشه وقتی به یک مشکل سخت میخوریم چنین راه حلهای دیوانه واری جواب نمی دهند. این راه حل استفاده از مقادیر تصادفی با نام جستجوی فراگیر(brute-force) نامیده می شود.بیشتر از این روشها برای نفوذ و کشف رمز های عبور استفاده می شود. بیشتر بر روی رمز های عبوری جواب میدهد که کلمات انگلیسی باشد و خیلی هم طولانی نباشد. کامپیوتر های خانگی امروزی با سرعت خوبی که دارند برای یک تست ۱۰۰۰۰ تایی از کلمات تصادفی به خوبی جواب می دهند.
اما در مورد شبکههای عصبی چطور؟ تصویر کنید همان شبکه عصبی با سه لایه و در هر لایه سه گره داریم. برای هر وزن بین -1 تا +1 هزار حالت میتوان متصور شد. مثلاً 0.501 یا 0.203 یا 0.999.
تعداد وزن ها برای لایه با سه گره و سه گره در هر لایه برابر با 18 وزن می شود. بنابراین ما داریم
18*1000=18000
اگر یک شبکه عصبی با پانصد گره در هر لایه داشته باشیم، ما پانصد میلیون حالت وزن برای تست داریم. اگر تست هر ترکیب تنها یک ثانیه طول بکشد، ۱۶ سال بروز رسانی وزن ها برای تنها یک نمونه آموزشی زمان میبیرد! اگر هزار نمونه یادگیری داشته باشیم میشود ۱۶۰۰۰ هزار سال!
همانطور که میبینید روش جستجوی فراگیر اصلاً در اینجا کاربردی نیست. در حقیقت وقتی تعداد لایه ها، گرهها یا حالتها برای وزن های گره زیاد میشود به سرعت کار خراب می شود.
این معما برای سالها در مقابل ارائه یک راه حل ریاضی برای حل آن مقاومت کرد و هیچکس نتوانست پاسخ کاملی برای آن ارائه دهد. بالاخره طی دهه ۱۹۶۰-۱۹۷۰ به صورت عملی حل شد. دیدگاههای مختلفی وجود دارد که چه کسی اولین بار آن را ساخته است و نکات کلیدی آن را کشف کرد. اما مهم این است که این کشف به انفجاری در شبکههای عصبی جدید انجامید که میتوانست وظایف خیلی ارزشمندی را انجام دهد.
خوب حالا چطور این مشکل سخت را حل می کنیم؟ باور کنید یا نکنید شما ابزار آن را برای اینکه خودتان آن را انجام دهید دارید. همه موضوع را پیشتر گفتیم. خوب بیایید سراغش برویم. اولین کاری که میکنیم این است که کاملاً بدبین و بد گمان باشیم.
معادله ریاضی نشان داد که همه نتایج وزن های لایه خروجی شبکه عصبی پیچیدهتر از آن است که قابل انجام باشد. ترکیب های ممکن آنقدر زیاد است که نمیتوان با تست یکی یکی آنها به بهترین نتیجه رسید.
دلیل های دیگری نیز داریم که بدبین باشیم. دادههای آموزشی ممکن است آنقدر کافی نبوده باشند که خوبی شبکه عصبی آموزش ببینید. دادههای آموزشی ممکن است حاوی خطا باشند. بنابراین به دادههای آموزشی اینطور نگاه نمیکنیم که صد در صد درست هستند، و میتوانیم کاملاً از آنها همه چیز را بیاموزیم. ممکن است اشتباه داشته باشند. خود شبکه عصبی هم ممکن است تعداد لایهها یا گرههای کافی برای مدل کردن کامل راه حل را نداشته باشند.
این به معنی آن است که ما باید یک روش واقعگرایانه را در پیش بگیریم و محدودیت ها را شناسایی کنیم. اگر ما این کار را انجام دهیم، ممکن است یک راه حلی را پیدا کنیم که شاید از منظر ریاضی خیلی عالی نباشد، اما در واقعیت نتیجه بهتری به ما میدهد. دلیل آن شاید این باشد که فرض های غلط ایده آل در آن لحاظ نشده است.
بیایید حرفهایی که زدیم را به تصویر بکشیم. تصور کنید روی یک سطح و زمین با پستی بلندی ها، صخره ها و دره ها، شکاف ها و بر آمدگی های زیاد هستید. هوا کاملاً تاریک است و شما نمیتوانید چیزی را ببینید. میدانید که بالای تپه هستید و باید به پایین آن خود را برسانید. نقشه درستی هم ندارید. تنها یک چراغ قوه دارید. چه کار می کنید؟ ممکن است از چراغ استفاده کنید ، آن را به سطح جلوی پایتان بتابانید. نمیتوانید از آن برای نگاه به جلوتر استفاده کنید. و نمیتوانید تمام سطح زمین را با آن ببینید. تنها میتوانید ببینید در نزدیکیتان کجا پایینتر است و به آن قسمت یک قدم کوچک بردارید و حرکت کنید. از این طریق کم کم کار راه خود را میابید و به پایین تپه می رسید. بدون اینکه یک نقشه کامل داشته باشید و یا اینکه قبلاً از آنجا گذر کرده باشید و با آنجا آشنا باشید.
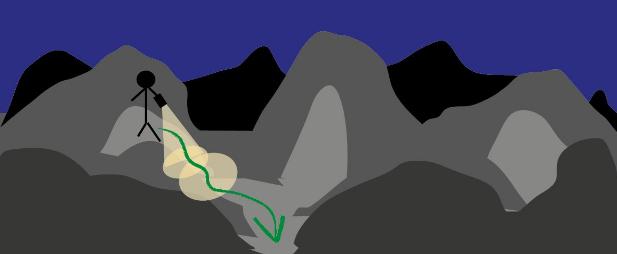
نسخه ریاضی همین روش با نام شیب نزولی (gradient descent) شناخته می شود. که کاملاً مشخص است که چرا این نام را دارد. بعد از اینکه یک قدم برداشتید، دوباره به اطراف نگاه میکنیم تا ببینیم کدام مسیر شما را به هدف نزدیکتر می کند. دوباره یک قدم به سمت مسیر بر میداریم. این کار را تا جایی که به پایین برسیم انجام میدهیم. شیب به ما جهت حرکت را نشان میدهد. در این جهت قدم میزنیم تا به پایینترین سطح شیب برسیم.
حالا تصور کنید که سطح پر از پستی و بلندی یک تابع ریاضی است. چیزی که شیوه شیب نزولی به ما میدهد این است که به ما امکان میدهد پایینترین نقطه را پیدا کنیم بدون اینکه نیاز باشد که آن تابع پیچیده را کامل بدانیم. اگر یک تابع خیلی پیچیده باشد ما به آسانی نمیتوانیم نقطه کمترین را با استفاده از محاسبات ریاضی بدست آوریم. به جای آن میشود از این روش استفاده کرد. مطمئناً ممکن است به جواب کاملاً درست نرسیم. به دلیل اینکه ما مرحطه به مرحله به جواب نزدیک شدیم و موقعیت خودمان را ذره به ذره بهبود دادیم. اما این بهتر از آن است که اصلاً هیچ جوابی نداشته باشیم. به هر ترتیب ، ما میتوانیم پاسخ خود را با برداشتن قدمهای کوچکی به سمت نقطه کمترین واقعی بهبود دهیم. تا جایی که از دقتی که به دست آوردیم راضی شویم.
چه ارتباطی بین شیوه جالب شیب نزولی و شبکههای عصبی وجود دارد؟
خوب اگر تابع پیچیده و سخت ما خطای شبکه باشد، پس پایین رفتن ما از تپه برای پیدا کردن نقطه کمترین به معنای حداقل رساندن خطا است.
ما خروجی شبکه را اینگونه بهبود می دهیم. چیزی که میخواستیم این است. اجازه بدهید ایده شیب نزولی را با یک مثال فوقالعاده ساده ببینیم. که آن را بهتر و به درستی متوجه شویم.
تصویر زیر یک تابع ساده
y=(x-1)2+1
را نشان میدهد
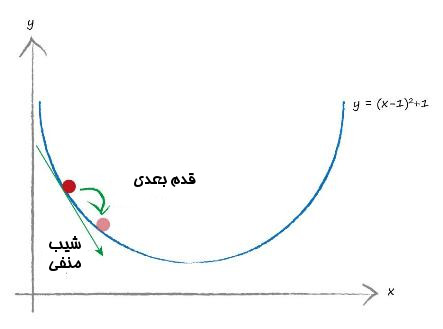
اگر این یک تابع باشد که در آن y خطا باشد.ما میخواهیم مقدار x را پیدا کنیم که y را به حداقل می رساند. برای یک لحظه فکر کنید که مثلاً این کار آسانی نیست و در عوض خیلی هم سخت است.
برای اینکه شیب نزولی را انجام دهیم از یک جایی باید شروع کنیم. تصویر نشان میدهد که ما یک نقطه تصادفی را به عنوان نقطه شروع در نظر گرفته ایم. شبیه به صخره نوردان ما به اطرافمان نگاه میکنیم و میبینیم چه مسیری به سمت پایین است. شیب در تصویر علامتگذاری شده است و در اینجا شیب منفی است. ما میخواهیم مسیر به سمت پایین را دنبال کنیم. پس ما روی محور x به سمت راست حرکت می کنیم.خودشه، مقدار x را کمی افزایش بدهیم. این اولین قدم صخره نورد ماست. شما میتوانید ببیند که موقعیت خود را کمی جابه جا کردیم و به مقدار کمینه و حداقلی که دنبال آن هستیم کمی نزدیکتر شدیم.
بیایید تصور کنیم اگر از جای دیگر شروع میکردیم چه می شد. مثل تصویر بعدی
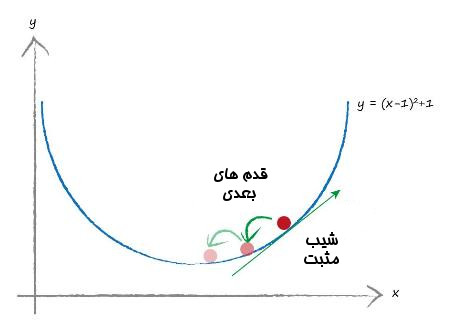
این بار، جهت شیب از نظر محور مختصات مثبت است. برای همین هم به جهت چپ حرکت می کنیم. پس همین مقدار x را کمی کاهش می دهیم. دوباره میبینیم که مقدار حداقل و کمینه واقعی نزدیکتر شدیم. این کار بهبود را آنقدر تکرار میکنیم تا جایی که از مقدار بدست آمده راضی باشیم و مقدار بدست آمده به کمینه واقعی خیلی نزدیک باشد.
یکی از نکاتی که به آن باید دقت کنیم این است که اندازه قدمها را به اندازهای کوچک برداریم که اتفاقی از مقدار کمینه رد نشویم و به آن طرف آن نرویم. میتوانید تصور کنید که اگر ما تنها نیم متر با مقدار کمینه واقعی فاصله داشته باشیم و یک قدم دو متری بردایم چه می شود. خوب مقدار کمینه را رد کردیم. اگر برنامه جوری باشد که تنها قدمهای دومتری بتواند بردارد نمیتوانیم به مقدار کمینه واقعی نزدیک شویم چون هر قدمی که بداریم از آن رد میشود. پس اندازه قدمها را باید کوچک کنیم تا بتوانیم به مقدار کمینه واقعی نزدیکتر شویم. میتوانیم یک فرض دیگر بگیریم که با نزدیک شدن به مقدار کمینه از مقدار شیب هم کم میشود. این فرض در اکثر تابع های نرم پیوسته (smooth continuous functions) درست است. به غیر از تابع های زیگ زاگی که شکلاف،فاصله و پستی بلندی زیاد دارند. ریاضی دانان به این تابع ها ناپیوسته (discontinuities) می گویند.
تصویر زیر ایده کوچکتر کردن قدمها را هنگامی که مقدار شیب کم میشود را نشان می دهد. اینکه چطور میتوانیم با تنظیم اندازه قدمها به مقدار کمینه نزدیکتر شویم.
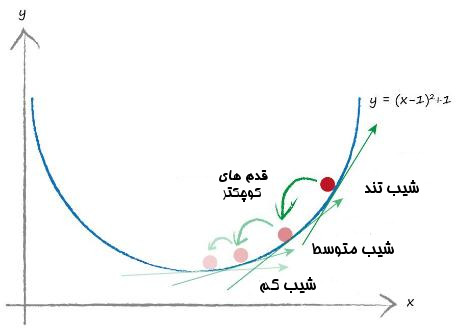
به هر ترتیب، آیا متوجه شدید که مقدار x را برخلاف جهت شیب تغییر می دهیم؟ یک شیب مثبت به معنای کاهش مقدار x است. یک شیب منفی هم به معنای افزایش x است. تصویر این موضوع را به وضوح نشان می دهد. اما این یکی از موضوعات فرار از ذهن است و ممکن است زود فراموشش کنید و در موقع نیاز اشتباه کنید.
وقتی که از شیب نزولی استفاده میکنیم، در حقیقت از ریاضیات دقیق استفاده نمی کنیم. در اینجا فرض کردیم که تابع
y=(x-1)2+1
خیلی پیچیده است و با روش ریاضی نمیتوان به آسانی آن را حل کردیم. حتی وقتی که نتوانیم مقدار شیب را به صورت دقیق با استفاده از ریاضیات به دست آوریم. میتوانیم آن را تخمین بزنیم. میبینید که این روش ما را در هدایت به مسیر صحیح به خوبی یاری می کند.
این شیوه وقتی خودش را به خوبی نشان میدهد که ما تابعی با پارامتر های خیلی زیاد داشته باشیم. در این موارد نه تنها y وابسته به x است بلکه وابسته به a ، b ، c ، d، e و f هم هست. تابع خروجی را بیاد بیاورید، پس تابع خطا در شبکههای عصبی هم به تعداد خیلی خیلی زیادی پارامتر وزن وابسته است. اغلب صدها پارامتر از وزن.
تصویر زیر دوباره همان شیب نزولی یا همان گرادیان دیسنت است. اما با تابع کمی پیچیدهتر که به دو پارامتر وابسته است. میشود در یک تصویر سه بعدی آن را به نمایش گذاشت که در آن ارتفاع مقدار تابع است.
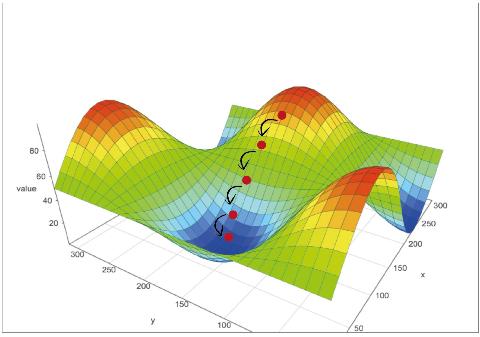
شما ممکن است به این تصویر سه بعدی نگاه کنید و بگویید آیا ممکن نیست که گرادیان نزولی در دره های دیگر تصویر گیر بیفتد؟ اگر تابع ما مثل بسیاری از تابع های پیچیده چند دره داشت چی؟ اصلاً دره اشتباه کدام است؟ کدام دره از همه عمیقتر است؟ از کجا بفهمیم دره را اشتباه پایین آمده ایم؟ پاسخ این است که بله. ممکن است این اتفاق بیفتد.
برای جلوگیری از این مشکل دره های اشتباهی در تابع کمینه سازی، ما شبکه عصبی خود را چندین بار با شروع از مکان های مختلف تپه آموزش میدهیم. تا مطمئن شویم که در دره اشتباهی نیستیم. نقاط شروع مختلف به معنی مقادیر متفاوت پارامتر ها در شروع هستند. در مورد شبکههای عصبی این به معنای وزن های شروع متفاوت برای لینک ها هستند.
تصویر زیر شروع متفاوت را برای شیب نزولی نشان میدهد. در اینجا یکی از آنها کار خود را با گیر افتادن در یک دره اشتباهی به پایان رسانده است.

بیایید مکث کنیم و افکارمان را جمع کنیم.
نکتههای کلیدی:
شیب نزولی یا همان گرادینت دیسنت ( gradient descent) یک روش خیلی خوب برای کمینه سازی تابع است. این روش بر روی تابع های خیلی پیچیده و سخت که با روشهای دیگر ریاضی حل آنها راحت نیست یا غیر عملی هستند.
علاوه بر این، این روش بر روی تابع هایی با تعداد پارامتر های خیلی زیاد به خوبی جواب می دهد. در جایی که خیلی از روشهای دیگر به شکست می انجامند و یا بسیار پر هزینه هستند.



دیدگاهها
ممنونم، خیلی خوب بود
خواهش می کنم
دیدگاه جدیدی بگذارید