پس انتشار خطاها با استفاده از روش ضرب ماتریس ها

آیا میتوانیم همانند قبل یک بار دیگر از ضرب ماتریس ها برای ساده کردن تمام این محاسبات پیچیده استفاده کنیم؟ پیشتر ما از آن برای محسبات مرتبط با سیگنال های ورودی و حرکت‌ رو به جلوی آن‌ها در لایه ها از آن استفاده کردیم.

 

برای اینکه ببینیم آیا امکان این است که از ضرب ماتریس راحت‌تر کردن باز انتشار خطا استفاده کنیم. بیایید بیایید مراحل را با نماد ها بنویسیم. نام این کار بردار سازی(vectorise) روند است.

اگر بتوانیم روند ها و داده‌ها را به صورت ماتریس در بیاوریم چند مزین دارد. اول اینکه نمایش آن به صورت خیلی مختصر تر قابل انجام است. دوم اینکه به رایانه ها اجازه می‌دهد به صورت بهینه تری انجام دهند. زیرا روند های تکراری برای انجام محاسبات داریم.

 

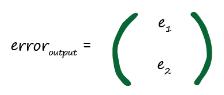
نقطه شروع محاسبه خطا در شبکه‌های عصبی در پایان کار لایه خروجی است. در اینجا ما دو گره در لایه خروجی داریم. بنابراین خطا های آن‌ها e1 و e2 نام گذاری کرده ایم.

 

در ادامه میخواهیم ماتریس خطا ها را برای لایه پنهان ایجاد کنیم. به نظر سخت می‌آید. اما بیایید آن را ذره ذره انجام دهیم.  اولین قسمت اولین گره در لایه پنهان است. اگر به تصویر بالا دوباره نگاه کنیم، میبینیم که اولین در خطای گره اول دو مسیر مشارکت داشته اند. آن‌ها خطای خروجی e1*w₁₁ و خطای خروجی e2*w₁₂ هستند. حالاه به گره دوم لایه پنهان نگاه کنید ما میتوانیم دوباره ببینیم که دو مسیر در خطای آن مشارکت داشته اند. خطا های e1*w₂₁ و e2*w₂₂. بنابراین ما ماتریس زیر را برای لایه پنهان داریم.

 

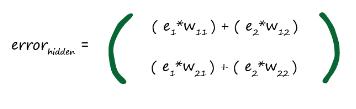
بعضی سریع متوجه این می‌شوند که می‌توانند از ضرب ماتریس ها استفاده کنند، بعضی دیگر کمی زمان میبرد تا متوجه آن شوند. این شکلی است:

 

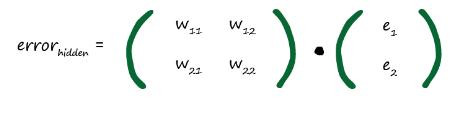
ماتریس وزن ها شبیه همانی است که قبل تر داشتیم اما به نظر برعکس شده است. الان این شکلی است که سمت راست بالا اکنون در سمت چپ پایین قرار دارد و پایین سمت چپ در سمت راست بالا قرار دارد. تغییر به این شکل یک ماتریس را با نام ترانهاده کردن یک ماتریس می گویند.  به ماتریسی که ترانهاده یک ماتریس دیگر است ماتریس ترانهاده می گویند. و آن را به شکل W^T نمایش می دهند.

 

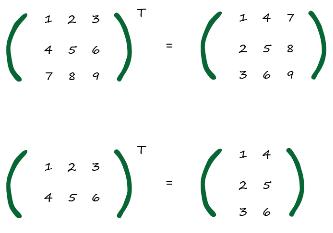
در زیر دو مثال از ترانهاده دو ماتریس اعداد آمده است. میتوانیم به وضوح ببینیم که چه اتفاقی افتاده است.  میتوانید ببینید که این کار را میتوان وقتی تعداد ستون‌ها و ردیف ها برابر نیست هم انجام دهید.

عالی. حالا ما یک نگاه ماتریس به پس انتشار خطا داریم:

 

خیلی از مسیر را رفتیم. واقعاً خوب شد.

 

 

 

قبل از ادامه خوب استراحت کنید. چون آخرین قسمت از فصل یک یعنی فصل مفاهیم تئوری واقعاً  جالب است. ولی نیاز به یک ذهن آماده و فعال دارد.