شما اینجا هستید
اعتراف کنیم که ضرب ماتریس ها برایمان مفید است
همه ما از ماتریس ها خاطرات وحشتناکی داریم. چه ساعتهایی که وقتمان را در مدرسه در حالی که دندان هایمان را روی هم فشار می دادیم به ضرب ماتریس می پرداختیم. بدون اینکه بفهمیم چه کار داریم انجام میدهیم و هدف خاصی داشته باشیم.
کمی قبل ما محاسبات دو لایه از نورون را با تنها دو گره در هر کدام از آنها به صورت دستی انجام دادیم. همان حد کافی بود. اما تصور کنید که همین کار را با شبکه هایی از ۵ لایه که در هر کدام از آنها صد ها گره وجود دارد بخواهیم انجام دهیم. نوشتن تمام این محاسبات کار سنگینی است… ضرب مقادیر تمام سیگنال ها در وزن ها و جمع زدن آنها و اعمال تابع فعال ساز سیگموئید روی آنها برای هر گره در هر لایه… ای خدا!
ماتریس چطور میتواند کمک کننده باشد؟ خوب از دو روش به ما کمک می کند. اول به ما اجازه میدهد تمام این محاسبات را به شکل کوتاه تری بنویسیم. که خیلی برای ما انسانها خوب است. به خاطر اینکه کار زیاد ما را خسته میکند و احتمال خطا را افزایش می دهد. نفع دومی که دارد این است که اکثر زبانهای برنامه نویسی کار با ماتریس ها را میفهمند. همچنین به خاطر اینکه این کار تکرار پذیر است میتوانند آنها را خیلی سریع و به صورت بهینه انجام دهند.
به صورت خلاصه، ماتریس ها به ما اجازه میدهند کاری که قرار است انجام شود را به صورت تمیزی نمایش دهیم و کامپیوتر ها میتوانند محاسبات را با استفاده از آن به صورت سریع و بهینه انجام دهند.
حالا میدانیم که چرا سراغ ماتریس ها رفتیم، با اینکه تجربه دردناکی برایمان از مدرسه باقیمانده اما بیایید باز هم یک تلاش دیگر داشته باشیم.
یک ماتریس فقط یک جدول است، یک شبکه مستطیل شکل از اعداد. فقط همین. هیچ چیز پیچیدهتری درباره ماتریس ها وجود ندارد.
اگر شما تا حالا از برنامههای صفحه گسترده مثل اکسل استفاده کرده باشید، پس با کار کردن با اعدادی که در لیست مرتب شدهاند راحت هستید. بعضی آن را جدول می نامند. میتوانیم آن را هم یک ماتریس بدانیم. در زیر یک صفحه گسترده با جدولی از اعداد آمده است.
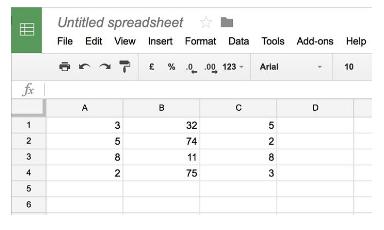
این همه آن چیزی است که یک ماتریس است. یک جدول یا شبکه ای از اعداد. مثل ماتریس نمونه زیر با اندازه «۲ در ۳».

به عنوان قرارداد ما اول تعداد ردیف ها را میگوییم بعد تعداد ستونها را. برای همین هم این یک ماتریس «۳ در ۲» نیست. این یک ماتریس «۲ در ۳» است. همچنین به هر کدام از عناصر ماتریس یک دَرایه میگویند. برای مشخص کردن هر درایه باید عدد ردیف و ستون آن را بصورت پاییننویس حرف کوچک نام ماتریس نوشت. برای نمونه اگر نام ماتریسی A باشد، درایهای که در ردیف اول و ستون دوم قرار دارد نوشته میشود a۱۲ و خوانده میشود "درایهی یک دو".
همچنین بعضی افراد از یک کروشه ها برای دور ماتریس ها استفاده می کنند، در حقیقت این فضا ها مجبور نیستند فقط با اعداد پر شوند. میتوانیم یک نام به جای آن بگذاریم که نشان میدهد قرار است چه چیزی در این قسمت قرار بگیرد. اما هنوز مقدار واقعی آن مشخص نیست. بنابراین در ماتریس زیر ، هر دَرایه یا عنصر یک متغیر است که به معنای آن است که میتواند یک مقدار عددی بگیرد. اما هنوز مقدار آن مشخص نیست.

حالا، در اینجا برای استفاده از ماتریس ها باید بدانیم که چگونه میتوانیم آنها را ضرب کنیم. ممکن است از مدرسه چیزهایی به خاطر داشته باشید. اگر نه ما دوباره نگاهی به آن خواهیم انداخت.
در اینجا یک مثال از دو ماتریس ساده که در هم ضرب شدهاند آمده است.
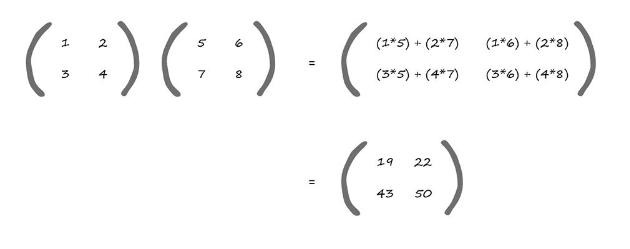
همانطور که میبینید ما فقط عناصر با موقعیت یکسان را در هم ضرب نکردیم.
گوشه بالا سمت چپ فقط با مقدار ۵*۱ نوشته نشده است، و گوشه پایین راست فقط ۸*۴ نیست.
به جای آن ماتریس ها قانون دیگری برای ضرب دارند. ممکن است با نگاه به مثال بالا این قانون را کشف کرده باشید. اگر نه، در تصویر زیر به جاهایی که رنگ شدهاند نگاه کنید. ببینید که چطور برای عنصر بالا سمت چپ کار انجام شده است.
همانطور که میبینید برای محاسبه عنصر بالا سمت چپ ما روی ردیف بالا از ماتریس اول و ستون اول ماتریس دوم کار کردیم.
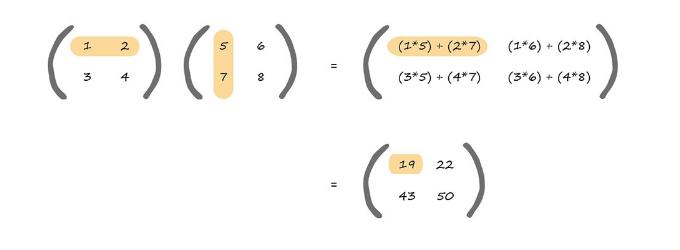
خوب بیایید ببینیم. با نگاه به ردیف اول سمت چپ از ماتریس اول ما مقدار ۱ را میبینیم. همینطور با نگاه به ستون اول از ماتریس دوم ما مقدار ۵ را میبینیم. پس ۱ را در ۵ ضرب میکنیم که خود ۵ میشود. نتیجه را نگه میداریم. ادامه میدهیم و عنصر دوم از ردیف اول ماتریس اول را با عنصر دوم از ستون اول ماتریس دوم را ضرب میکنیم یعنی ۲ و ۷ که میشود ۱۴ و نتیجه را نگه میداریم. حالا که به پایان ردیف و ستون رسیدیم.این نتایج را با هم جمع می کنیم. ۵+۱۴ برابر ۱۹. این برای محاسبه عنصر بالا سمت چپ از ماتریس نتیجه بود.
خیلی حرف زدیم. بهتر این است که در عمل ببینیم.در زیر برای محاسبه عنصر پایین سمت راست کار انجام شده نشان داده است.
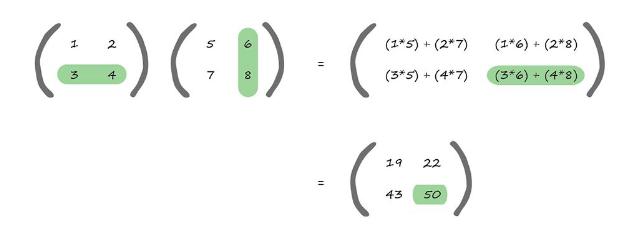
شما میتوانید دوباره ردیف و ستونهای مرتبط با عنصری را که میخواهیم محاسبه کنیم را ببینید.( ردیف دوم از از ماتریس اول و ستون دوم از ماتریس دوم) که برابر با (3*6) و (4*8) میشود و در نهایت 18 + 32 = 50.
برای تکمیل موضوع ، برای عنصر پایین چپ (3*5) + (4*7) = 15 + 28 = 43 و برای عنصر بالا راست (1*6) + (2*8) = 6 + 16 = 22.
ادامه قانون محاسبه را با متغیر ها به جای اعداد آوردیم.
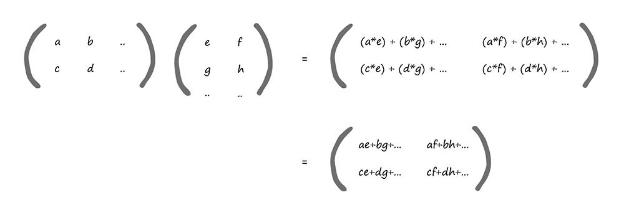
این هم یک روش دیگر برای توضیح شیوه ضرب ماتریس ها است. با استفاده از حروف، که میتوان جای آن هر عددی را گذاشت. این تصویر به معنی یک رویکرد عمومی است. یعنی میتوان آن را برای هر ماتریسی به هر اندازهای اعمال کرد.
وقتی ما میگوییم این برای ماتریس ها در هر اندازهای کار می کند. یک محدودیت جدی نیز وجود دارد. نمیشود هر دو ماتریسی را در هم ضرب کرد. باید با هم جور باشند. شاید این موضوع را موقعی که داشتید عناصر هر ردیف از ماتریس اول را در ستون مربوطه در ماتریس دوم ضرب میکردید متوجه شده باشید.
اگر تعداد عناصر ردیف ماتریس اول برابر با تعداد عناصر ستون ماتریس دوم نباشد، این روش هم کار نمی کند. خوب پس نمیشود که یک ماتریس ۲*۲ را در یک ماتریس ۵*۵ ضرب کرد. باور ندارید امتحان کنید. میبینید که کار نمی کند. خلاصه در ضرب ماتریس ها تعداد ستونها در ماتریس اول باید برابر تعداد ردیف ها در ماتریس دوم باشد
در بعضی راهنما ها، شما این نوع ضرب ماتریس ها را با نام ضرب نقطهای(dot product) یا ضرب داخلی(inner product) می بینید. انواع مختلف دیگری از ضرب ماتریس ها وجود دارند مثل ضرب خارجی(cross product). اما آن چیزی که ما اینجا لازم داریم ضرب نقطهای است.
چه شد که مثل یک خرگوش در تله ضرب ماتریس ها و محاسبات بی مزه آن افتادیم؟ یک دلیل خوب وجود دارد. یک طعمه خوش مزه اینجا آویزان بود.
ببینید چه میشود اگر ما حروف را با کلماتی که در شبکههای عصبی برای ما بامعنا هستند جایگزین کنیم. ماتریس دوم یک ماتریس دو در یک است، اما روش ضرب یکسان است. برای ورودی ها input و برای وزن ها w نوشتیم
اجی مجی لا ترجی
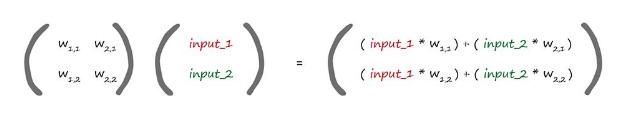
ماتریس اول حاوی وزن های بین گرهها در دو لایه است. ماتریس دوم سیگنال های ورودی لایه اول است. نتیجه ضرب بین دو ماتریس ترکیب ضرب سیگنال های ورودی تعدیل شده در گرهها در لایه دوم است.
خوب نگاه کنید. شما آن را میبینید. در اولین گره اولین ورودی با نام first_1 آمده که با وزن w1,1 تعدیل شده است و با ورودی دو که با نام input_2 آمده و در وزن w2,1 تعدیل شده است. در نهایت با هم جمع شده اند. خوب اینهمان چیزی بود که ما در برای محاسبه x انجام میدادیم . قبل از اینکه تابع فعال ساز سیگموئید را روی آن اعمال کنیم.
تصویر زیر این موضوع را واضح تر نشان می دهد.
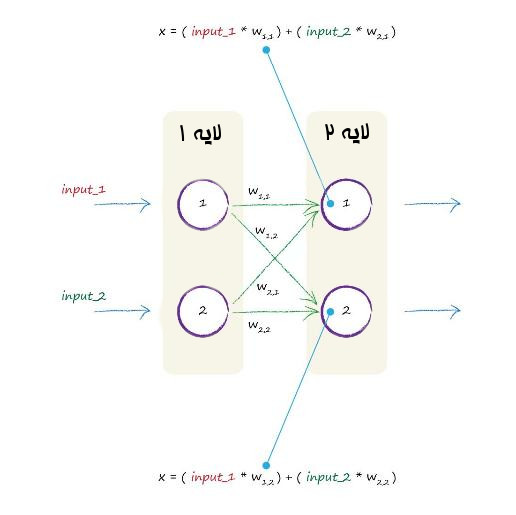
خیلی به کارمان می آید.
چرا؟ چون تمام آن محاسباتی که قبل تر برای ترکیب وزن ها و سیگنال ها و جمع آنها برای هر گره در لایه دوم را انجام دادیم را میتوانیم به صورت یک ضرب ماتریس نمایش دهیم. بعد هم میشود به راحتی این عبارت را برای آن نوشت:
X=W·I
به همین راحتی، در اینجا W ماتریس وزن هاست، I ماتریس ورودی هاست و X یعنی نتیجه ضرب نقطهای این دو میشود: ماتریس مقادیر تعدیل شده سیگنال های ورودی در لایه دوم.
حالا دیگر مهم نیست که چه تعداد گره در هر لایه داریم. هرچقدر تعداد گرهها زیاد باشد، فقط ماتریس بزرگتر می شود. ما نمیخواهد چیزی را طولانیتر و طولانیتر بنویسیم.فقط کافی است بنویسیم W.I ، حالا تعداد عنصار میخواد ۲ تا باشد یا ۲۰۰ تا.
حالا اگر زبان برنامه نویسی ما علایم ماتریسی را درک کند، تمام کارهای سخت محاسبات را با نوشتن X = W.I برای ما انجام می دهد. بدون اینکه بخواهیم برای هر گره دستور العمل جدایی برای آن بنویسیم.
خیلی معرکه است. واقعاً به سختی فهمیدن ضرب ماتریس ها می ارزید. حالا ابزار قدرتمندی داریم که میتوانیم روی شبکههای عصبی خودمان اعمال کنیم بدون اینکه برای ما زحمت محاسبه ایجاد کند.
خوب پس تابع فعال ساز چی؟ این کار راحت است و نیازی به ضرب ماتریس ها نیست. تنها کاری که باید انجام دهیم این است که تابع فعال ساز سیگموئید را روی هر عنصر ماتریس X اعمال کنیم.
زیادی ساده به نظر می رسد.ولی کار درستی هم هست. چرا که ما سیگنال های ورودی به گرههای مختلف را با هم ترکیب نکردیم. سیگنال های ورودی به یک گره را در وزن های آنها ضرب کردیم و با هم جمع کردیم. در نهایت نتیجه را برای هر گره در جای خودش در ماتریس X قرار دادیم. همانطور که گفتیم تابع فعال ساز یک آستانه و دیوار برای مقادیر ورودی است. مانند آنچه در نورون های زیستی می بینیم. اگر مقادیر بزرگتر از دیوار باشند میتوانند از روی آن رد شوند. بنابراین خروجی نهایی به این صورت میباشند.
O=sigmoid(X)
حرف O که به صورت پررنگ نوشته شده خودش یک ماتریس است. که حاوی تمامی مقادیر خروجی در لایه آخر شبکه عصبی است. معادله X = W·I بر روی یک لایه و لایه بعدی آن اعمال می شود. اگر ما ۳ لایه داشته باشیم. برای مثال ما به سادگی ضرب ماتریس ها را دوباره و دوباره انجام می دهیم. به این شکل این کار را میکنیم که خروجی لایه دوم به عنوان ورودی لایه سوم محاسبه میشود و البته وزن های تعدیل مرتبط در هر ارتباط در این لایه نیز روی آن اعمال می شود. تئوری بس است – بیایید ببینم در یک مثال واقعی چطوری کار می کند. اما این بار از یک شبکه عصبی بزرگتر با سه لایه که در هر لایه سه گره وجود دارد استفاده می کنیم.
نکات کلیدی:
محاسبات خیلی زیادی که برای ارسال یک سیگنال در شبکه عصبی لازم است را میتوان به شکل ضرب ماتریس ها نشان داد.
نمایش آن به صورت ضرب ماتریس ها بدون توجه به اندازه آن برای ما خیلی راحتتر است.
از آن مهمتر ، بعضی زبانهای برنامه نویسی محاسبات ماتریس ها را درک میکنند و میتوانند آن را انجام دهند. چون کارهای مورد نیاز خیلی تکراری و شبیه به هم هستند. برای همین هم میتوانند خیلی سریع و به صورت بهینه آن را انجام دهند.



دیدگاه جدیدی بگذارید